صلح خبر – سجاد جوهردلوری: مقدار عدد گنگ پی ۳.۱۴۱۵۹۲۶۵۳ میباشد؛ همیشه همین بوده و همیشه همین خواهد بود؛ با ارقام اعشاری نامحدود. مقدار محیط یک دایره تقسیم بر قطرش همواره پی و مقدار پی همواره ۳.۱۴۱۵۹ خواهد بود؛ با همان ارقام اعشاری نامحدود. اما این موضوع باعث نشد که شخصی به نام ادوارد گودوین برای باز تعریف آن به ۳.۲ و البته به صورت قانونی تلاش نکند.

این فرد بدون شک یا بسیار شوخ بوده یا اینکه ریاضیدانی ساده و آماتور که گمان میکرده تغییری سرنوشت‌ساز انجام داده است. به هر صورت این قصه‌ی عجیب حقیقت دارد. در سال ۱۸۹۷ گودوین بر این باور بود که مقدار جدید و صحیح و دقیق پی را پیدا کرده است و در تلاش بود تا این کشف! خود را به شکل قانون در بیاورد.

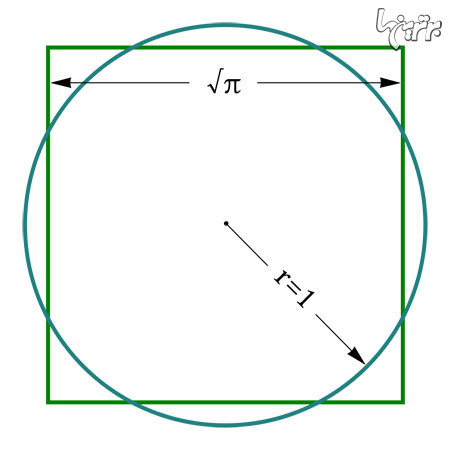
گودوین به خصوص باور داشت که توانسته است با موفقیت دایره را چهارگوش کند؛ چهار گوش کردن دایره معماییست که از زمان یونان باستان ریاضیدانان را مشغول خود کرده است. این معما به این معناست که بتوان مربعی با محیط یک دایره ترسیم کرد. به دلیل اینکه محیط یک دایره شامل عددی غریب و شگفت چون پی میباشد ریاضیدانان امروزی و مدرن به خوبی فهمیده‌اند و میدانند که این کار شدنی نیست. طول ضلع‌های مربع در اینصورت باید عددی گنگ چون پی باشند و این امکان‌پذیر نیست. عقیده‌ی گودوین بر این بود که این کار شدنیست چرا که پی ۳.۱۴۱۵۹ با اعشاری نامحدود نیست بلکه ۳.۲ است.

در خاطرات پروفسور سی‌ای‌والدو که ریاضیدانی مورد احترام و معاصر ادوارد گودوین بود آمده است که قانون پیشنهادی وی بسیار بی‌معنی بود اما با اینحال شامل چندین رقم پیشنهادی برای عدد پی میشد. در ابتدا انتخاب عدد ۴ بررسی شده بود و کم کم و در پایان به عدد ۳.۲ رسید. این طرح به دلیل دخالت به موقع این ریاضیدان برجسته که هنگام رای‌ گیری در صحن مجلس سنا حضور داشته است تصویب نمیشود.

باور کنید یا نه این طرح با همه‌ی اشتباهاتش راه درازی را برای درک این اشتباه بودنش پیمود. اولین کمیته‌ی دریافت کننده اصلا نتوانست بفهمد که با آن چه باید کرد و به همین دلیل آن را به کمیته‌ی آموزش فرستادند. این کمیته به طرز غیر قابل درکی در فوریه‌ی ۱۸۹۷ آن را برای رای گیری به مجلس نمایندگان فرستاد. پس از این که سه بار در صحن مجلس قرائت شد به طریقی بدون مقاومت و باز هم غیر قابل درک پذیرفته شد. در نهایت در مجلس سنا رای نیاورد و متوقف شد آنهم نه به خاطر اشتباه بودنش بلکه به این خاطر که  قوانین بدیهی ریاضی را نمیتوان تغییر داد و به صورت قانون در آورد. خوش به حال ریاضیات.